0.前言
世界上没有普世的,放之四海皆准的算法。但是人们在日常生活中总结出了可以适应大多数场景的,相对比较好的算法。今天就简单介绍一下其中比较著名的支持向量机。
1.线性可分与线性不可分
介绍支持向量机之前,先明白两个概念,线性可分(Linear Separable)和线性不可分(Nonlinear Separable)。
什么是线性可分?比如下面这张图片就是一个二维的线性可分图像:
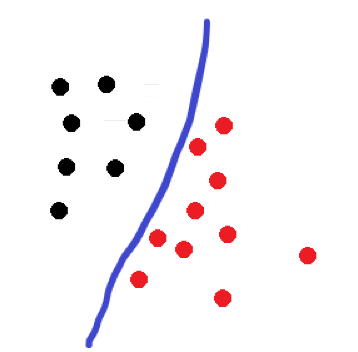
图中大致可分为两类,一类是红色,一类是黑色。这样的数据样本集可以被一条直线分隔开(实际上有多条直线可以把红色和黑色分隔开),我们认为这样的数据数据集就是线性可分的。
同理,如果一个样本集不存在上面的这样的直线可以把数据集分成两部分,则称为非线性可分的。
我们也可以把二维图像扩展成三维的图像。
我们借助下面的数学公式来表示线性可分与线性不可分问题。
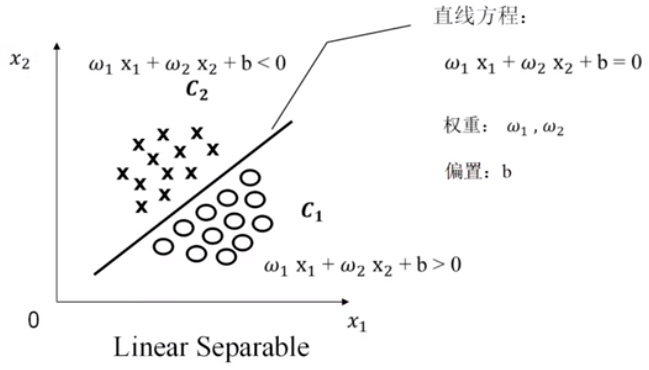
对于上面这个图像,圆圈用C1表示,叉号用C2表示。中间的直线方程可以用
$$w_1 + w_2 + b =0 $$ 。那么在直线上方的我们假设认为小于零 $$w_1 + w_2 + b <0 $$,在直线下方的我们认为大于0, $$w_1 + w_2 + b >0 $$。
我们认为,$w_1 $和$w_2$称为$x_1$ 和$x_2$的权重,$b$称为偏置。
注意上面的一点,我们只是认为上方小于0,下方大于0。但是这只是我们人为规定的,我们同样可以认为上方大于0,下方小于0。
那么。假设我们有N个这样的训练样本和他们的标签:
$$ {(X_1,y_1),(X_2,y_2),(X_3,y_3),…,(X_N,y_N)} $$
其中 $$ X_i =[x_i1,x_i2]^T$$ $$ y_i={+1 或-1}$$
则,我们可以用数学严格定义线性可分:一个训练样本集$$ {(X_i,y_i),…,(X_N,y_N)}$$ 在$$i=1-N $$ 线性可分,是指存在$$ (w_1,w_2,b)$$ 使得对$$i=1-N $$有
(1)若$$ y_i = 1$$ 则$$w_1 + w_2 + b >0 $$。
(2) 若$$ y_i = -1$$ 则$$w_1 + w_2 + b <0 $$。
2.支持向量机解决的问题
支持向量机解决的问题主要分为下面两种。
1.解决线性可分问题
2.再将线性可分问题中获得的结论推广到线性不可分的情况。
详细来说。如果一个数据集是线性可分的,那么将存在无数多个超平面将数据分开,最好的是哪一个呢。比如下面这张图像:
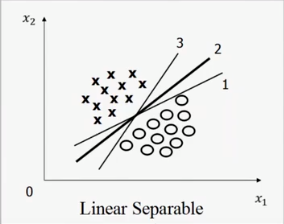
有三条线,1,2,3,哪一条线是最好的?
有一种解释是2号线对于样本的误差的容忍程度是最高的,如果从这个方面来考虑则2号线是最好的。
那么,继续考虑一个问题,我们假设的这个二号线是如何画出来的(这也就是支持向量机的由来)?
假设对于任意一条能够分开圆圈和叉的直线,我们把这条直线(必须是平行于原来的直线)朝着两侧分别移动,当移动到快要接触到点或者叉(实际上就是两种不同的数据集)。比如下面这样:
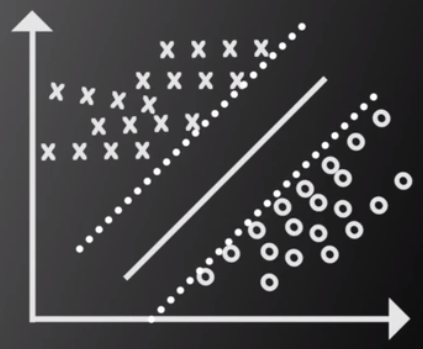
我们认为这两条线遇到圈或者叉号的时候停止。这时候,我们称与这两条线相交的圈或者叉叫做支持向量。两条线之间的距离叫做间隔。
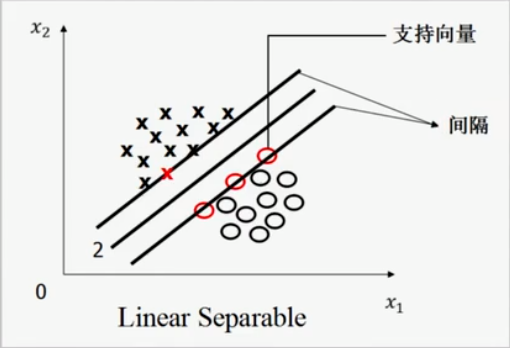
我们的目的就是让间隔最大的那条线(图中所示的2号线。)
那么问题来了,按照上图是说法,所有平行与2号线且没有与任意数据集相交的直线都符合条件,怎么保证直线的唯一性。
再加一个条件,要找的目的直线距离左右两边的距离相等,这样就能保证唯一性。
总结:
(1)该直线分开了直线。
(2)该直线最大化间隔。
(3)该直线处于间隔的中间,到所有支持向量距离相等。
3.支持向量机的定义
根据上面描述的总结,支持向量机主要是一种二分类的模型。官方定义如下:
支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器。